Magnitude and Frequency Scaling
Last modified: Oct, 2013
Magnitude and frequency scaling is very useful when designing filters. Given an existing design (e.g., a low-pass filter with certain low-cutoff frequency, and of course, the values of resistor, capacitor and inductor), one can use scaling and quickly calculate the values of R, C and L for another similar design but with different cut-off frequency.
The scaling relationships are:
where R, L, C are the initial values, R’, L’ and C’ are the scaled values, \( s_m \) is the magnitude scaling factor, and sf is the frequency scaling factor.
How does it work? A general procedure is first set cut-off frequency \( \omega_0 \) to 1 rad/s, and set some component values to easy numbers, such as 1F or 1 Ohm. Calculate the other component values based on that. Finally, scale everything to the ones you want.
There are two examples below:
Example 1: simple RC filter
Consider a simple RC low-pass filter like this:

This is a low-pass filter with 3dB bandwidth of
or
Now, I need to design a similar filter with 3dB bandwidth of 1kHz, and I want to use a 1nF capacitor instead. The question is: what resistor value should I use? First I calculate the frequency scaling factor:
and then calculate the magnitude scaling factor
At last, the new resistor value should be
Example 2: Sallen-Key active filter
The previous example is just a very simple example with lumped elements. The simple principle can be used in more complex cases, such as Salley-Key active filters. Take the 2nd-order high-pass Butterworth filter for example as below:
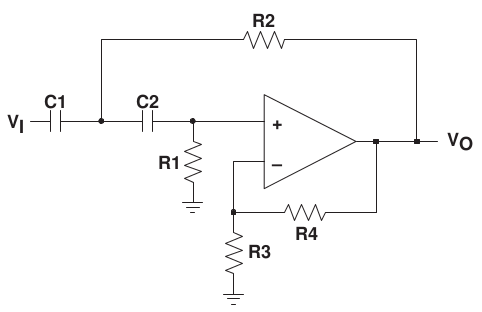
with transfer function
where
and
For the convenience, first set the cut-off frequency
and both capacitors C1 and C2 to 1F. Then the Q is reduced to
Since Q= \( \frac{\sqrt{2}}{2} \) for Butterworth filter, we can solve R1 and R2 from the equations:
The solutions can be easily got like this:
Now, if I want to design a Sallen-Key unity-gain (H0=1) Butterworth filter with cut-off frequency of 1kHz, using capacitors 1uF, what are the values of resistors? This can be easily done with scaling techniques as follows.
First find the frequency scaling factor:
Then calculate the magnitude scaling factor:
Therefore, the two resistor values are: